Composite material testing: How do I know if my measured composite properties are correct, or even reasonable?

Those familiar with mechanical testing of composite materials are well aware of the challenges associated with proper testing and accurate measurement of their mechanical properties. To date, many of my columns have focused on such challenges associated with specific types of tests performed with composite materials. In this column, we explore ways to determine whether the properties obtained from mechanical testing of composites are correct — or even reasonable. We’ll focus on the more fundamental types of mechanical tests performed on unidirectional fiber-reinforced composites to measure their stiffness and strength properties.

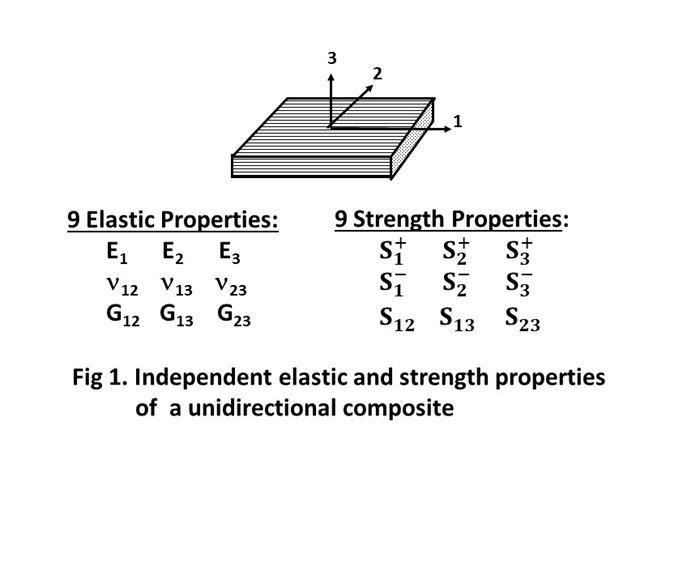
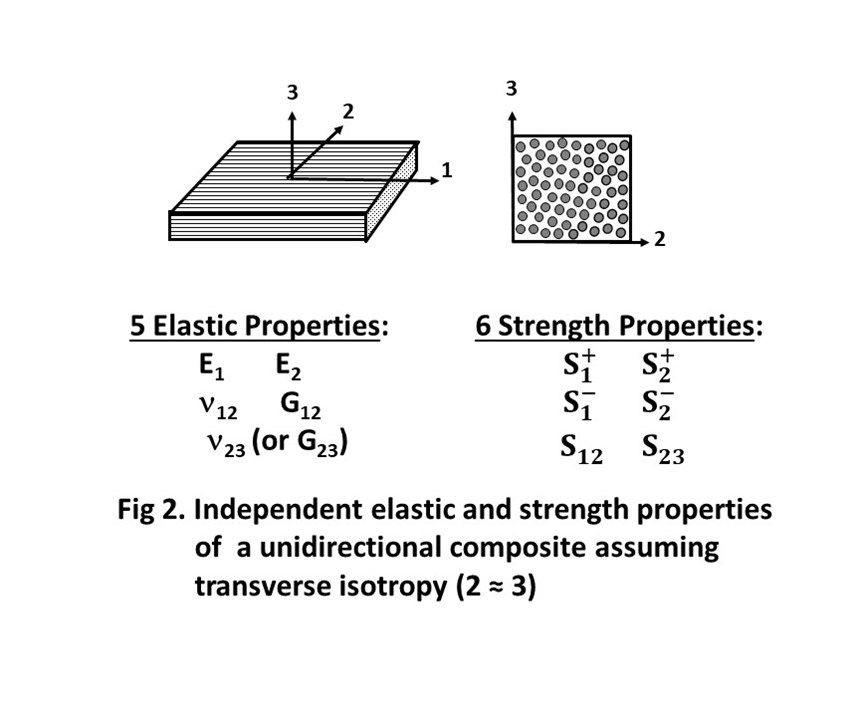
Stiffness properties, also referred to as elastic properties, include the modulus of elasticity E, the shear modulus G and Poisson’s ratio ν. For isotropic materials such as metals and plastics, stiffness properties are independent of material orientation and thus only one value exists for each of these three stiffness properties. In contrast, the stiffness properties of unidirectional fiber-reinforced composites are highly dependent on the fiber orientation relative to the applied force. To fully characterize the material stiffness of composites, tests must be performed at three mutually perpendicular material orientations relative to the applied loading, resulting in three values for each stiffness property (Fig. 1). However, when multiple layers of 0° prepreg are cured together to make a multilayer unidirectional composite, the random distribution of fibers between the layers causes transverse isotropy in the plane perpendicular to the fiber direction (the 2 and 3 directions shown in Fig. 2). This causes the material to have the same stiffness when pulled in either a horizontal or vertical direction, making several of the stiffness properties redundant. So, of the nine stiffness properties for a unidirectional composite material, the number of independent stiffness properties that must be measured may be reduced to five if the unidirectional composite is assumed to be transversely isotropic¹ (Fig. 2).

In addition to stiffness properties, the strength properties of a unidirectional fiber-reinforced composite are also highly dependent on the material orientation relative to the applied force. Additionally, the strength properties can be significantly different under tension and compression loading due to different possible failure modes that can occur. Although there are a total of nine strength properties for a unidirectional composite, the number of independent strength properties is reduced to six under the assumption of transverse isotropy¹ (Fig. 2), because the material shows the same properties in all directions.  In contrast, metals typically require only two strength properties be measured: tension and shear strength.

After measuring any of these stiffness or strength properties for a unidirectional fiber-reinforced composite, how do we determine if the measured value is correct … or even reasonable? A common starting point is to look for published test results from the same material, or a material that is considered similar. Fortunately, there are several publicly available sources of material property information for composites. For example, a composite material supplier’s data sheets are one source of such information. They typically report fiber-direction stiffness and strength properties under tension and compression loading, as well as in-plane shear properties. Some material properties may also be provided at environmental conditions other than room temperature.

Publicly available databases are another resource. For example, the Advanced General Aviation Transport Experiments (AGATE) database² was developed for commonly used composites in the general aviation industry in the 1990s. The online AGATE database includes lamina material properties for carbon fiber- and glass fiber-reinforced composites with woven fabric and unidirectional fibers. Additionally, the follow-on National Center for Advanced Materials Performance (NCAMP) database³, initiated in 2005, expanded its focus to the general aerospace industry. The online NCAMP database includes lamina and laminate property data for a variety of composite materials. Finally, mechanical property data for a variety of composite material of general interest is available in Volume 2 of the Composite Materials Handbook (CMH-17)⁴, which is available for purchase from SAE International.

Even though sources of mechanical property information is available for many composites, there are considerably more possible fiber and matrix combinations currently available. Thus it may not be possible to find published information about the desired mechanical properties for a particular composite material of interest. Additionally, since the mechanical properties depend to various degrees on the processing method and fiber volume fraction of the composite, they may not be representative of the as-fabricated material of interest. Further, similar composite materials, perhaps with the same type of fiber but with a different matrix material, may not have similar material properties. Some mechanical properties, such as the fiber-direction (0°) tension stiffness E₁ and tension strength S₁⁺ , typically are fiber-dominated such that the choice of a similar polymer matrix material does not produce a significant difference. However, other mechanical properties such as the 90° tension stiffness E₂ and tension strength S₂⁺ are more matrix-dominated properties, and may not be affected significantly when used with a similar fiber. Additionally, the fiber-direction (0°) compression strength S₁^-  depends on the fiber and matrix, as the matrix material provides resistance to fiber microbuckling, the typical failure mode under an applied compression force. Thus an apparently similar composite material may not produce similar mechanical properties.

Despite the challenges associated with using reference material property values to assess whether test results are correct, they are of value in determining whether the results are reasonable. Material properties from these data sheets and databases may provide a feel for the approximate magnitudes and the amount of variability in the mechanical properties of interest for composites with fiber variations, matrix material variations or both.

In addition to using published data, two mechanical properties of unidirectional composites may be predicted relatively accurately based on properties of the fiber and matrix, as well as the fiber volume fraction of the composite. The fiber-direction (0°) stiffness E₁ and tension strength S₁⁺ may be calculated using a simple rule-of-mixtures equation derived from a constant-strain “springs in parallel” model¹. The modulus E₁ may be calculated using the equation

E₁ = (E_f) (v_f)  +  (E_m)(v_m),

where the subscripts f and m denote fiber and matrix properties, respectively, and v is the volume fraction of the constituents. Similarly, the fiber-direction tensile strength S₁⁺ of a unidirectional composite may be calculated from the same constant strain model using the equation

S₁⁺  = (S_f⁺)  (v_f)  +  (S_m⁺) (v_m).

Using these equations, the fiber-direction stiffness and strength of a unidirectional composite can be approximated with reasonable accuracy simply by knowing the fiber stiffness and strength as well as the volume fraction of the constituents.

References

¹Gibson, R. F. “Principles of Composite Material Mechanics,” 4th Edition, CRC Press, 2016.

²Advanced General Aviation Transport Experiments (AGATE) database, www.niar.wichita.edu/agate/

³National Center for Advanced Materials Performance  (NCAMP) database, www.niar.wichita.edu/coe/ncamp.asp

⁴Composite Materials Handbook - 17 (CMH-17), Volume 2: Materials Properties, SAE International, Rev. G, 2012.